


Back to: List of Publications
Automatic Labeling of Self-Organizing Maps:
Making a Treasure-Map Reveal its Secrets
Andreas Rauber and Dieter Merkl
Institut für Softwaretechnik, Technische Universität Wien
Resselgasse 3/188, A-1040 Wien, Austria
{andi, dieter}@ifs.tuwien.ac.at
Abstract:
Self-organizing maps are an unsupervised neural network model which lends itself to the cluster analysis of high-dimensional input data.
However, interpreting a trained map proves to be difficult because the features responsible for a specific cluster assignment are not evident from the resulting map representation.
In this paper we present our
LabelSOM approach for automatically labeling a trained self-organizing map with the features of the input data that are the most relevant ones for the assignment of a set of input data to a particular cluster.
The resulting labeled map allows the user to better understand the structure and the information available in the map and the reason for a specific map organization, especially when only little prior information on the data set and its characteristics is available.
The self-organizing map (SOM) [2,3] is a prominent unsupervised neural network model for cluster analysis.
Data from a high-dimensional input space is mapped onto a usually two-dimensional output space with the structure of the input data being preserved as faithfully as possible.
This characteristic is the reason why the SOM found large attraction for its utilization in a wide range of application arenas.
However, its use in the knowledge discovery domain has been limited due to some drawbacks in the interpretability of a trained SOM.
As one of the shortcomings we have to mention the difficulties in detecting the cluster boundaries within the map.
This problem has been addressed intensively and led to a number of enhanced visualization techniques allowing an intuitive interpretation of the self-organizing map, e.g. the U-Matrix [10], Adaptive Coordinates [6] and Cluster Connection techniques [5].
However, it still remains a challenging task to label the map, i.e. to determine the features that are characteristic for a particular cluster. Given an unknown data set that is mapped onto a self-organizing map, even with the visualization of clear cluster boundaries it remains a non-trivial task to elicit the features that are the most relevant and determining ones for a group of input data to form a cluster of its own, which features they share and which features distinguish them from other clusters.
We are looking for a method that allows the automatic assignment of labels describing every node in the map.
A method addressing this problem using component planes for visualizing the contribution of each variable in the organization of a map has been presented recently [1].
This method, however, requires heavy manual interaction by examining each dimension separately and does thus not offer itself to automatic labeling of SOMs trained with high-dimensional input data.
In this paper we present our novel LabelSOM approach to the automatic labeling of trained self-organizing maps.
In a nutshell, every unit of the map is labeled with the features that best characterize all the data points which are mapped onto that particular node.
This is achieved by using a combination of the mean quantization error of every feature and the relative importance of that feature in the weight vector of the node.
We demonstrate the benefits of this approach by labeling a SOM that was trained with a widely used reference data set describing animals by various attributes.
The resulting labeled SOM gives a description of the animals mapped onto nodes and characterizes the various (sub)clusters present in the data set.
We further provide a real-world example in the field of text mining based on a digital library SOM trained with the abstracts of scientific publications. This SOM represents a map of the scientific publications with the labels serving as a description of their topics and thus the various research fields.
The remainder of the paper is organized as follows.
In Section 2 we present a brief review of the self-organizing map, its architecture and training process as well as the LabelSOM method to assign a set of labels for every node in a trained SOM and provide results from a well known reference data set.
In Section 3 we provide the results of applying the LabelSOM method to a real world data set labeling a map representing the abstracts of scientific publications. We further demonstrate how additional information on the cluster structure can be derived from the information provided by the labeling.
A discussion of the presented LabelSOM method as well as its importance for the area of knowledge discovery and data mining is provided in Section 4.
Finally, our conclusions are presented in Section 5.
Automatic Labeling of Self-Organizing Maps:
Making a Treasure-Map Reveal its Secrets
Andreas Rauber and Dieter Merkl
Institut für Softwaretechnik, Technische Universität Wien
Resselgasse 3/188, A-1040 Wien, Austria
{andi, dieter}@ifs.tuwien.ac.at
Abstract:
Self-organizing maps are an unsupervised neural network model which lends itself to the cluster analysis of high-dimensional input data.
However, interpreting a trained map proves to be difficult because the features responsible for a specific cluster assignment are not evident from the resulting map representation.
In this paper we present our
LabelSOM approach for automatically labeling a trained self-organizing map with the features of the input data that are the most relevant ones for the assignment of a set of input data to a particular cluster.
The resulting labeled map allows the user to better understand the structure and the information available in the map and the reason for a specific map organization, especially when only little prior information on the data set and its characteristics is available.
The self-organizing map (SOM) [2,3] is a prominent unsupervised neural network model for cluster analysis.
Data from a high-dimensional input space is mapped onto a usually two-dimensional output space with the structure of the input data being preserved as faithfully as possible.
This characteristic is the reason why the SOM found large attraction for its utilization in a wide range of application arenas.
However, its use in the knowledge discovery domain has been limited due to some drawbacks in the interpretability of a trained SOM.
As one of the shortcomings we have to mention the difficulties in detecting the cluster boundaries within the map.
This problem has been addressed intensively and led to a number of enhanced visualization techniques allowing an intuitive interpretation of the self-organizing map, e.g. the U-Matrix [10], Adaptive Coordinates [6] and Cluster Connection techniques [5].
However, it still remains a challenging task to label the map, i.e. to determine the features that are characteristic for a particular cluster. Given an unknown data set that is mapped onto a self-organizing map, even with the visualization of clear cluster boundaries it remains a non-trivial task to elicit the features that are the most relevant and determining ones for a group of input data to form a cluster of its own, which features they share and which features distinguish them from other clusters.
We are looking for a method that allows the automatic assignment of labels describing every node in the map.
A method addressing this problem using component planes for visualizing the contribution of each variable in the organization of a map has been presented recently [1].
This method, however, requires heavy manual interaction by examining each dimension separately and does thus not offer itself to automatic labeling of SOMs trained with high-dimensional input data.
In this paper we present our novel LabelSOM approach to the automatic labeling of trained self-organizing maps.
In a nutshell, every unit of the map is labeled with the features that best characterize all the data points which are mapped onto that particular node.
This is achieved by using a combination of the mean quantization error of every feature and the relative importance of that feature in the weight vector of the node.
We demonstrate the benefits of this approach by labeling a SOM that was trained with a widely used reference data set describing animals by various attributes.
The resulting labeled SOM gives a description of the animals mapped onto nodes and characterizes the various (sub)clusters present in the data set.
We further provide a real-world example in the field of text mining based on a digital library SOM trained with the abstracts of scientific publications. This SOM represents a map of the scientific publications with the labels serving as a description of their topics and thus the various research fields.
The remainder of the paper is organized as follows.
In Section 2 we present a brief review of the self-organizing map, its architecture and training process as well as the LabelSOM method to assign a set of labels for every node in a trained SOM and provide results from a well known reference data set.
In Section 3 we provide the results of applying the LabelSOM method to a real world data set labeling a map representing the abstracts of scientific publications. We further demonstrate how additional information on the cluster structure can be derived from the information provided by the labeling.
A discussion of the presented LabelSOM method as well as its importance for the area of knowledge discovery and data mining is provided in Section 4.
Finally, our conclusions are presented in Section 5.
SOM and LabelSOM
The self-organizing map is an unsupervised neural network providing a mapping from a high-dimensional input space to a usually two-dimensional output space while preserving topological relations as faithfully as possible.
The SOM consists of a set of i nodes arranged in a two-dimensional grid, with a weight vector
 attached to each node.
Elements from the high dimensional input space, referred to as input vectors
attached to each node.
Elements from the high dimensional input space, referred to as input vectors
 ,
are presented to the SOM and the activation of each node for the presented input vector is calculated using an activation function.
Commonly, the Euclidean distance between the weight vector of the node and the input vector serves as the activation function.
In the next step, the weight vector of the node showing the highest activation (i.e. the smallest Euclidean distance) is selected as the `winner' c and is modified as to more closely resemble the presented input vector.
Pragmatically speaking, the weight vector of the winner is moved towards the presented input signal by a certain fraction of the Euclidean distance as indicated by a time-decreasing learning rate
,
are presented to the SOM and the activation of each node for the presented input vector is calculated using an activation function.
Commonly, the Euclidean distance between the weight vector of the node and the input vector serves as the activation function.
In the next step, the weight vector of the node showing the highest activation (i.e. the smallest Euclidean distance) is selected as the `winner' c and is modified as to more closely resemble the presented input vector.
Pragmatically speaking, the weight vector of the winner is moved towards the presented input signal by a certain fraction of the Euclidean distance as indicated by a time-decreasing learning rate 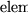 .
Thus this node's activation will be even higher the next time the same input signal is presented.
Furthermore, the weight vectors of nodes in the neighborhood of the winner are modified accordingly, yet to a less strong amount as compared to the winner.
This learning procedure finally leads to a topologically ordered mapping of the presented input signals, i.e. similar input signals are mapped onto neighboring regions of the map.
.
Thus this node's activation will be even higher the next time the same input signal is presented.
Furthermore, the weight vectors of nodes in the neighborhood of the winner are modified accordingly, yet to a less strong amount as compared to the winner.
This learning procedure finally leads to a topologically ordered mapping of the presented input signals, i.e. similar input signals are mapped onto neighboring regions of the map.
Still, the characteristics of each node are not detectable from the map representation itself.
With no a priori knowledge on the data, even providing information on the cluster boundaries does not reveal information on the relevance of single attributes for the clustering and classification process.
In the LabelSOM approach we determine those vector elements (i.e. features of the input space) that are most relevant for the mapping of an input vector onto a specific node.
This is basically done by determining the contribution of every element in the vector towards the overall Euclidean distance between an input vector and the winners' weight vector.
The LabelSOM method is built upon the observation that after SOM training the weight vector elements resemble as far as possible the corresponding input vector elements of all input signals that are mapped onto this particular node as well as to some extent those of the input signals mapped onto neighboring nodes. Vector elements having about the same value within the set of input vectors mapped onto a certain node describe the node in so far as they denominate a common feature of all data signals of this node. If a majority of input signals mapped onto a particular node exhibit a highly similar input vector value for a particular feature, the corresponding weight vector value will be highly similar as well. Thus the quantization error for all individual features serves as a guide for their relevance as a class label.
However, in real world text mining application scenarios we are usually faced with a high number of attributes which are not existent and thus have a value of 0 for a certain class of input signals.
These attributes frequently yield a quantization error of almost 0 for certain nodes but are nevertheless not suitable for labeling the node.
The reason is, that we want to describe the present features that are responsible for a certain clustering rather than describe a cluster via the features that are not present in the data forming that cluster.
Hence, we need to determine those vector elements from each weight vector which, on the one hand, exhibit about the same value for all input signals mapped onto that specific node as well as, on the other hand, have a high overall value indicating its importance. Formally this is done as follows:
Let Ci be the set of input patterns xj mapped onto node i.
Summing up the distances for each vector element over all the vectors xj (
 )
yields a quantization error vector qi for every node (Equation 1).
)
yields a quantization error vector qi for every node (Equation 1).
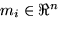 |
(2) |
To create a set of p labels for every node i we take the p smallest vector elements from the quantization error vector qi. In order to get rid of labels describing non-existent features we define a threshold 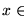 and take only features having corresponding weight vector entries above
and take only features having corresponding weight vector entries above 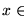 .
The threshold is typically set to very small values slightly above 0.
.
The threshold is typically set to very small values slightly above 0.
Table 1:
Input Data Set: Animals
|
Attribute |
Dove |
Hen |
Duck |
Goose |
Owl |
Hawk |
Eagle |
Fox |
Dog |
Wolf |
Cat |
Tiger |
Lion |
Horse |
Zebra |
Cow |
| is |
small |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
| |
medium |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
| |
big |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
| has |
2 legs |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| |
4 legs |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| |
hair |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| |
hooves |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
| |
mane |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
| |
feathers |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| likes to |
hunt |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
| |
run |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
| |
fly |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| |
swim |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Figure:
Labeling of a 6  6 SOM trained with the animals data set.
a.) Standard Representation of SOM b.) 5 labels assigned to each node of the SOM
6 SOM trained with the animals data set.
a.) Standard Representation of SOM b.) 5 labels assigned to each node of the SOM
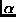 |
Figure 1 shows the result of labeling a
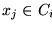 SOM trained with the animals data set [8] given in Table 1. (Please note that the input vectors have been normalized to unit length prior to the training process.)
The standard representation of the resulting SOM is given in Figure 1a, where each node is assigned the name of the input vectors that were mapped onto it.
In the resulting map we find a clear separation of the birds in the upper part of the map from the mammals in the lower area.
However, this conclusion can only be drawn if one has prior knowledge about the data and can thus infer the characteristic features of sets of input data from their name.
SOM trained with the animals data set [8] given in Table 1. (Please note that the input vectors have been normalized to unit length prior to the training process.)
The standard representation of the resulting SOM is given in Figure 1a, where each node is assigned the name of the input vectors that were mapped onto it.
In the resulting map we find a clear separation of the birds in the upper part of the map from the mammals in the lower area.
However, this conclusion can only be drawn if one has prior knowledge about the data and can thus infer the characteristic features of sets of input data from their name.
In Figure 1b, each node is assigned a set of 5 labels based on the quantization error vector and the value of the vector element.
We find that each animal is labeled with its characteristic attributes.
In addition to the information to be drawn from the characterization of the data points mapped onto the nodes, further information on the cluster boundaries can be derived, such as the fact that the birds are distinguished from the mammals by the fact that the all have 2 legs and feathers instead of 4 legs and hair.
Further subclusters are identified by the size of the animals and their preferences for /em hunting, flying, swimming, etc. For example, the big mammals being located in the lower right corner of the map as a subcluster of the mammals.
As another subcluster consider the distinction of hunting vs. non-hunting animals - irrespective of their belonging to the group of birds or group of mammals.
The hunting animals may be found on the left side of the map whereas the non-hunting animals are located on the right side.
Thus we can not only identify the decisive attributes for the assignment of every input signal to a specific node but also detect the cluster boundaries between nodes that are not winner for any specific input signal and tell the characteristics and extents of subclusters within the map.
Mind that not all nodes have the full set of 5 labels assigned, i.e. one or more labels are empty (none) like the node representing the dog in the lower right corner.
This is due to the fact that less than 5 vector elements have a weight vector value mik greater than 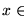 .
.
A Labeled Library SOM
For the following larger example we used 48 publications from the Department of Software Technology which are available via our department web server (www.ifs.tuwien.ac.at/ifs/).
We used full-text indexing to represent the various documents.
The indexing process identified 482 content terms, i.e. terms used for document representation.
During indexing we omitted terms that appear in less than 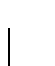 or more than
or more than 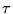 of all documents and applied some basic stemming rules.
The terms are weighted according to a simple
of all documents and applied some basic stemming rules.
The terms are weighted according to a simple
 weighting scheme [9].
weighting scheme [9].
In the area of digital libraries we are faced with a tremendous amount of 'noise' in the input data resulting from the indexing of free-form documents.
In the example presented thereafter another problem originates in the fact that abstracts contain little to no redundancy in terms of the information presented in the abstracts as well as in the choice of words.
Due to their limited length and condensed structure, word repetition and clarification of the most important aspects within the text usually are not present, resulting in less specific vector representations of the documents.
Thus using only the abstracts provides a somewhat more challenging task than using the complete documents.
For some deeper discussion on the utilization of SOMs in text data mining we refer to [7,4].
Figure:
Standard Representation of a 7  7 SOM trained with paper abstracts
7 SOM trained with paper abstracts
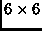 |
Figure:
Labeling of a 7  7 SOM trained with paper abstracts
7 SOM trained with paper abstracts
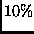 |
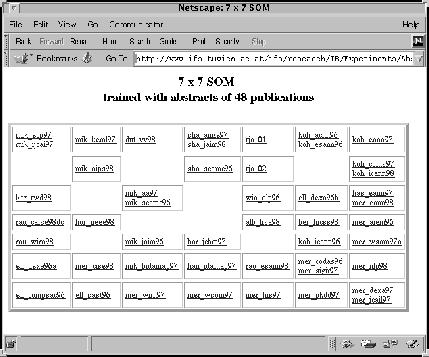
Figure 2 depicts a
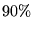 SOM trained with the 48 abstracts.
The various nodes again list the input vectors, i.e. the abstracts, that were mapped onto the nodes. The naming convention for the abstracts is such as to give the name of the first author of a paper as the first three characters, followed by the short form label of the respective conference.
SOM trained with the 48 abstracts.
The various nodes again list the input vectors, i.e. the abstracts, that were mapped onto the nodes. The naming convention for the abstracts is such as to give the name of the first author of a paper as the first three characters, followed by the short form label of the respective conference.
Without any additional knowledge on the underlying documents, the resulting mapping of the SOM given in Figure 2 is hard to interpret, although the names of the authors may give some hints towards the cluster structure of the map
(at least if you know the authors and have some knowledge concerning their research areas).
However, no information on the contents of the papers, i.e. the keywords, can be drawn from the resulting map.
With a weight vector dimensionality of 482, manual inspection of the importance of the single vector elements simply is not feasible.
Having a set of 10 labels automatically assigned to the the single nodes in Figure 3 leaves us with a somewhat clearer picture of the underlying text archive and allows us to understand the reasons for a certain cluster assignment as well as identify overlapping topics and areas of interest within the document collection.
For example, in the upper left corner we find a group of nodes sharing labels like skeletal plans, clinical, guideline, patient, health which deal with the development and representation of skeletal plans for medical applications.
Another homogeneous cluster can be found in the upper right corner which is identified by labels like gait, pattern, malfunction and deals with the analysis of human gait patterns to identify malfunctions and supporting diagnosis and therapy.
A set of nodes in the lower left corner of the map is identified by a group of labels containing among others software, process, reuse and identifies a group of papers dealing with software process models and software reuse.
This is followed by a large cluster to the right labeled with cluster, intuitive, document, archive, text, input containing papers on cluster visualization and its application in the context of document archives.
Further clusters can be identified in the center of the map on plan validation, and quality analysis, neural networks, etc.
To present a more detailed example, the node representing the abstract koh_icann98 (node (7/2) in the upper right part of the map) is labeled with the following keywords:gait, pattern, platform, aiming, bio-feedback, effects, diseases, active, compensation, employ.
The full text of the abstract is given in Figure 4.
It is obvious, that the labels derived from the LabelSOM approach describe the contents of the paper to a sufficient degree.
Figure 4:
Abstract of koh_icann98
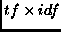 |
Figure 5:
Cluster identification based on labels
 |
Using these labels as class identifiers clear cluster boundaries can be defined by combining nodes sharing a set of labels.
This results in a total of 8 different clusters as shown in Figure 5.
Discussion
While the labels identified by our LabelSOM method in the text data mining example can probably not serve directly as a kind of class labeling in the conventional sense, they reveal a wealth of information about the underlying map and the structures learned during the self-organizing training process.
Groups of nodes having a set of labels in common help to determine the cluster structure within the map.
This can be used to provide an improved way of cluster boundary and map structure analysis and visualization by grouping and coloring nodes according to the common set of labels.
The benefit of determining cluster boundaries with the LabelSOM method lies with the fact that in addition to the mere cluster structure, the user gets a justification for the clustering as well as information on the sub-structure within clusters by the very attributes.
The labels themselves aid in identifying the most important features within every node and thus help to understand the information represented by a particular node.
In spite of the little redundancy present in abstracts, the labels turn out to be informative in so far as they help the user to understand the map and the data set as such.
Especially in cases where little to no knowledge on the data set itself is available, the resulting representation can lead to tremendous benefits in understanding the characteristics of the data set.
It is important to mention that the information used for the labeling originates entirely from the self-organizing process of the SOM without the use of sophisticated machine learning techniques which might provide further improved labeling capabilities.
Still, with the increasing use of self-organizing maps in the data mining area, the automatic labeling of resulting maps to identify the features of certain clusters based on the training process itself becomes an important aid in correctly applying the process and interpreting the results.
Being based on a neural network approach with high noise tolerance allows the application of the LabelSOM approach in a wide range of domains, especially in the analysis of very high-dimensional input spaces.
Conclusion
We have presented the LabelSOM method to automatically assign labels to the nodes of a trained self-organizing map. This is achieved by determining those features from the high-dimensional feature space that are the most relevant ones for a certain input data to be assigned to a particular cluster.
The resulting benefits are twofold:
First, assigning labels to each node helps with the interpretation of single clusters by making the common features of a set of data signals that are mapped onto the same node explicit.
This serves as a description for each set of data mapped onto a node.
Second, by taking a look at groups of (neighboring) nodes sharing common labels it is possible to determine sets of nodes forming larger clusters, to identify cluster and sub-cluster boundaries and to provide specific information on the differences between clusters. Finally, labeling the map allows it to be actually read.
- 1
-
S. Kaski, J. Nikkilä, and T. Kohonen.
Methods for interpreting a self-organized map in data analysis.
In Proc. 6th European Symposium on Artificial Neural Networks
(ESANN98). D-Facto, Brugfes, Belgium, 1998.
- 2
-
T. Kohonen.
Self-organized formation of topologically correct feature maps.
Biological Cybernetics, 43, 1982.
Springer Verlag, Berlin, Heidelberg, New York.
- 3
-
T. Kohonen.
Self-Organizing Maps.
Springer Verlag, Berlin, Germany, 1995.
- 4
-
D. Merkl.
Text classification with self-organizing maps: Some lessons learned.
Neurocomputing, 21(1-3), 1998.
- 5
-
D. Merkl and A. Rauber.
Cluster connections - a visualization technique to reveal cluster
boundaries in self-organizing maps.
In Proc 9th Italian Workshop on Neural Nets (WIRN97), Vietri
sul Mare, Italy, 1997.
- 6
-
D. Merkl and A. Rauber.
On the similarity of eagles, hawks, and cows - Visualization of
similarity in self-organizing maps.
In Proc. of the Int'l. Workshop on Fuzzy-Neuro-Systems '97
(FNS97), Soest, Germany, 1997.
- 7
-
A. Rauber and D. Merkl.
Creating an order in distributed digital libraries by integrating
independent self-organizing maps.
In Proc. Int'l Conf. on Artificial Neural Networks
(ICANN'98), Skövde, Sweden, 1998.
- 8
-
H. Ritter and T. Kohonen.
Self-organizing semantic maps.
Biological Cybernetics, 61:241 - 254, 1989.
Springer Verlag.
- 9
-
G. Salton.
Automatic Text Processing: The Transformation, Analysis, and
Retrieval of Information by Computer.
Addison-Wesley, Reading, MA, 1989.
- 10
-
A. Ultsch.
Self-organizing neural networks for visualization and classification.
In Information and Classification. Concepts, Methods and
Application. Springer Verlag, 1993.
A. Rauber and D. Merkl.
Automatic Labeling of Self-Organizing Maps: Making a Treasure-Map Reveal its Secrets
In Proceedings of the 3. Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD'99), Bejing, China, April 26-28, 1999.
LNCS / Lecture Notes in Artificial Intelligence, LNAI 1574, pp. 228 - 237, Springer Verlag
Automatic Labeling of Self-Organizing Maps:
Making a Treasure-Map Reveal its Secrets
This document was generated using the
LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)
Copyright © 1993, 1994, 1995, 1996, 1997,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 rau_pakdd99.tex.
The translation was initiated by Andreas RAUBER on 1999-05-06



Andreas RAUBER
1999-05-06
 attached to each node.
Elements from the high dimensional input space, referred to as input vectors
attached to each node.
Elements from the high dimensional input space, referred to as input vectors
 ,
are presented to the SOM and the activation of each node for the presented input vector is calculated using an activation function.
Commonly, the Euclidean distance between the weight vector of the node and the input vector serves as the activation function.
In the next step, the weight vector of the node showing the highest activation (i.e. the smallest Euclidean distance) is selected as the `winner' c and is modified as to more closely resemble the presented input vector.
Pragmatically speaking, the weight vector of the winner is moved towards the presented input signal by a certain fraction of the Euclidean distance as indicated by a time-decreasing learning rate
,
are presented to the SOM and the activation of each node for the presented input vector is calculated using an activation function.
Commonly, the Euclidean distance between the weight vector of the node and the input vector serves as the activation function.
In the next step, the weight vector of the node showing the highest activation (i.e. the smallest Euclidean distance) is selected as the `winner' c and is modified as to more closely resemble the presented input vector.
Pragmatically speaking, the weight vector of the winner is moved towards the presented input signal by a certain fraction of the Euclidean distance as indicated by a time-decreasing learning rate  or more than
or more than 